In a previous post, I showed how it was possible to crudely measure the speed of light (or at least another type of electromagnetic radiation, radio waves, in this case) by measuring the time delay between two shortwave radio time stations, WWV and WWVH.
I’ve decided to re-do that experiment, but in a slightly different way. Rather than measure the speed of propagation, I will use that speed to determine the distance to the radio station.
Various time stations transmit precise time on several shortwave frequencies. Here in the USA, we have WWV in Ft. Collins, Colorado, which transmits on 2.5, 5, 10, 15, and 20 MHz. We also have WWVH in Kekaha, Hawaii, which transmits on 2.5, 5, 10, and 15 MHz. These stations transmit an audio “tick” at exactly each UTC second. There is also the Canadian station CHU, located near Ottawa, Ontario, which transmits on 3330, 7850, and 14670 kHz.
One way to measure the speed of radio waves (and light) would be to measure how long it takes for the tick to travel a fixed distance. Divide the distance by the time, and we have the speed of light. However, that requires knowing the exact UTC time locally. This can be done with a GPS unit that outputs a 1 PPS (pulse per second) signal.
How to feed these signals into the computer, so they can be measured? The radio audio is easy enough, feed it into the sound card. It turns out the 1 PPS signal can also be fed into the sound card, on the other channel. I used a capacitor to couple it.
The first measurement that is required is one to determine what time delay is added by the radio electronics. In my case, I was using a JRC NRD 545 receiver, which has DSP (Digital Signal Processing) to implement the audio filters. This certainly adds a time delay. I therefore needed to run some baseline measurements, to determine how long this delay was.
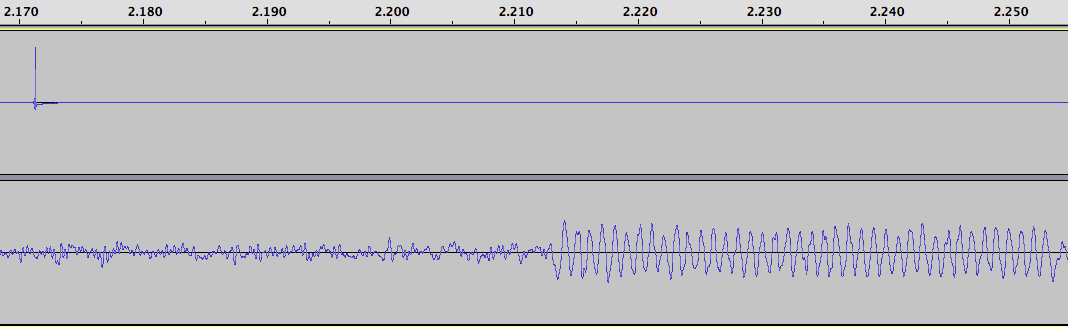
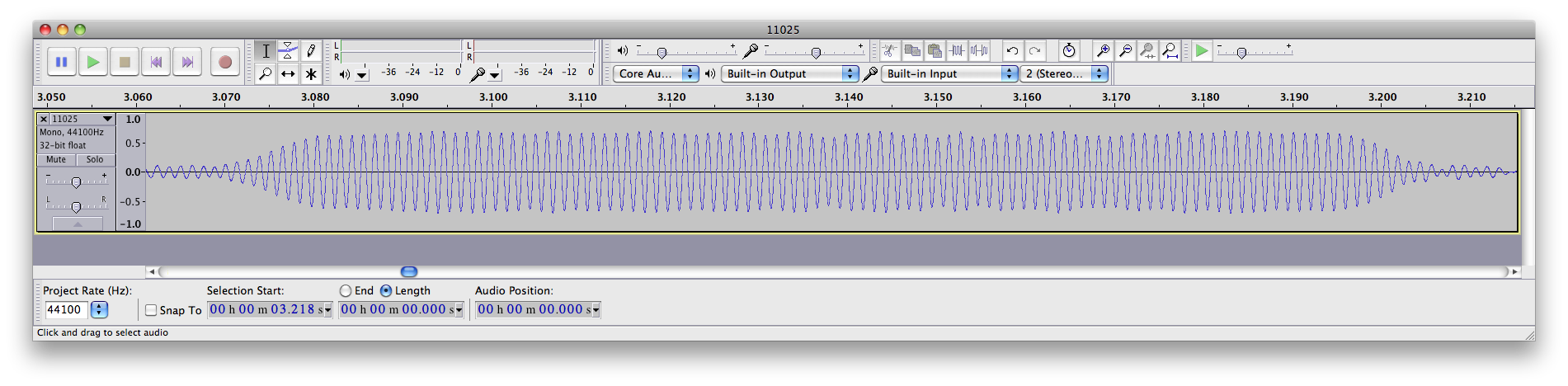
I fed the same 1 PPS signal into the antenna jack of the radio. The signal is a short (10 microsecond pulse) that is rich in harmonics, so it produces a noticeable “tick” sound every second. I then recorded the audio from the radio, along with the 1 PPS signal fed into the other channel, and obtained this data (click on the graph to enlarge it):
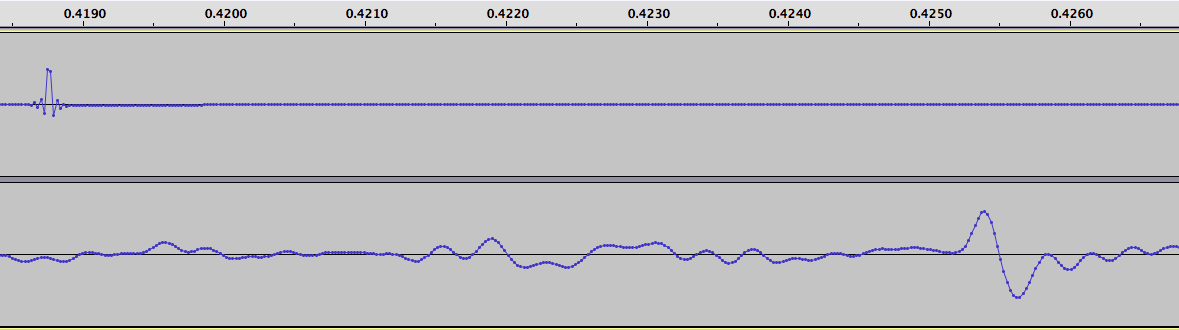
I measured the time delay between the two ticks, and found it to be 286 samples. At 44.1 kHz, each sound sample is 22.676 microseconds. Multiplication gives us the time delay, namely 6485 microseconds. This delay added by the radio is constant, provided I do not adjust the IF filtering parameters (which were set to USB mode, 4.0 kHz wide, for all tests).
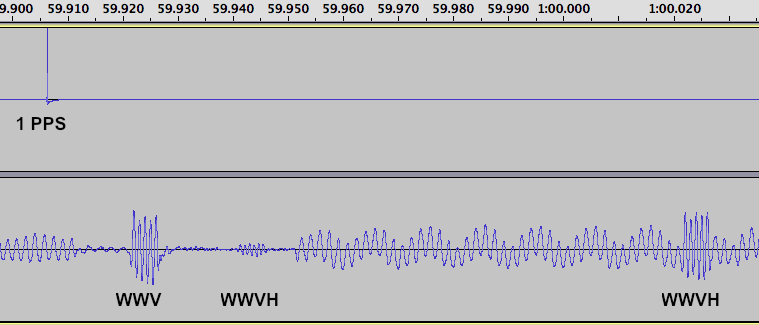
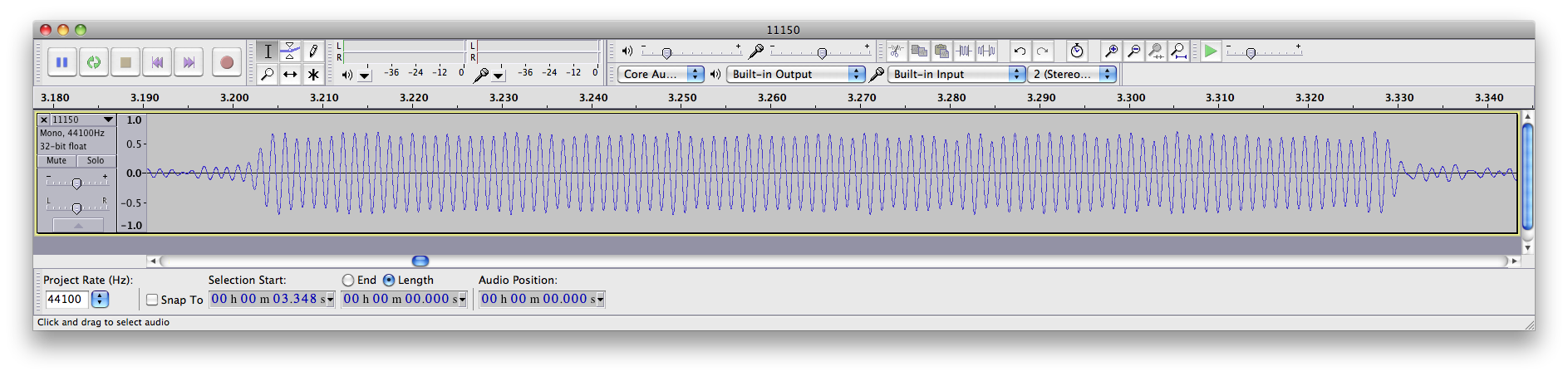
Next, the antenna was reconnected, an the radio tuned to 15 MHz. At this time of the day (about 2100 UTC) it is possible to hear both WWV and WWVH. Here’s the sound recording:
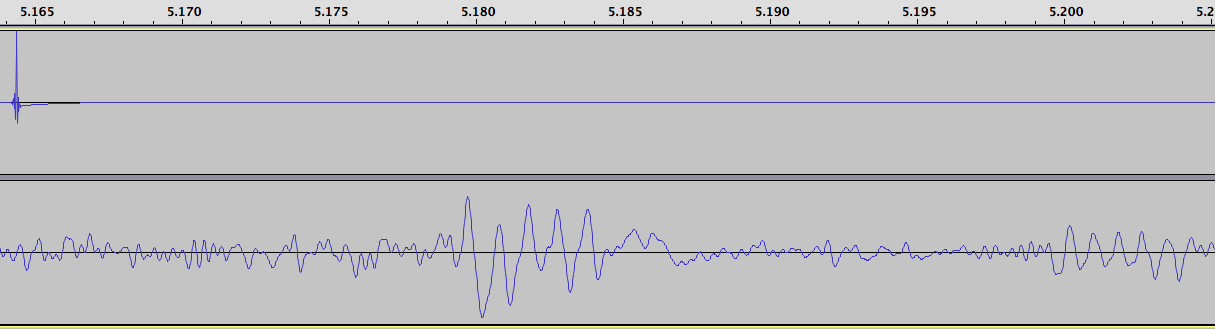
The WWV pulse occurs at about 5.18 seconds on the recording, and WWVH, much weaker and harder to see, at about 5.2 seconds.
The delay for the WWV pulse is 657 samples. Subtracting the radio delay of 286 gives us a delay due to propagation of 371 samples. Multiplying by our conversion factor of 22.676 microseconds per sample gives us 8413 microseconds.
Light (and radio waves) travel at 186,282 miles per second or about 0.186 miles per microsecond. For the metric inclined, that’s 299.792 km/sec or 0.300 km per microsecond. So multiplying our time in microseconds by the distance light travels each microsecond gives us the distance:
8413 * 0.186 = 1567 miles (2522 km)
The actual distance, along the Earth’s surface, from my location to WWV is 1480 miles, or 2382 km. Why the discrepancy? The radio waves do not travel along the Earth’s surface, but instead are reflected from the ionosphere, which is several hundred miles up. This means the actual path they take is longer. We’ll try to take that into account, a little further down.
The delay for the WWVH pulse is 1550 samples. Subtracting the radio delay of 286 gives us a delay due to propagation of 1264 samples. Multiplying by our conversion factor of 22.676 microseconds per sample gives us 28662 microseconds. We’ll do our next multiplication again, to convert to distance:
28662 * 0.186 = 5339 miles (8592 km)
The actual distance from my location to WWVH is 4743 miles, or 7633 km.
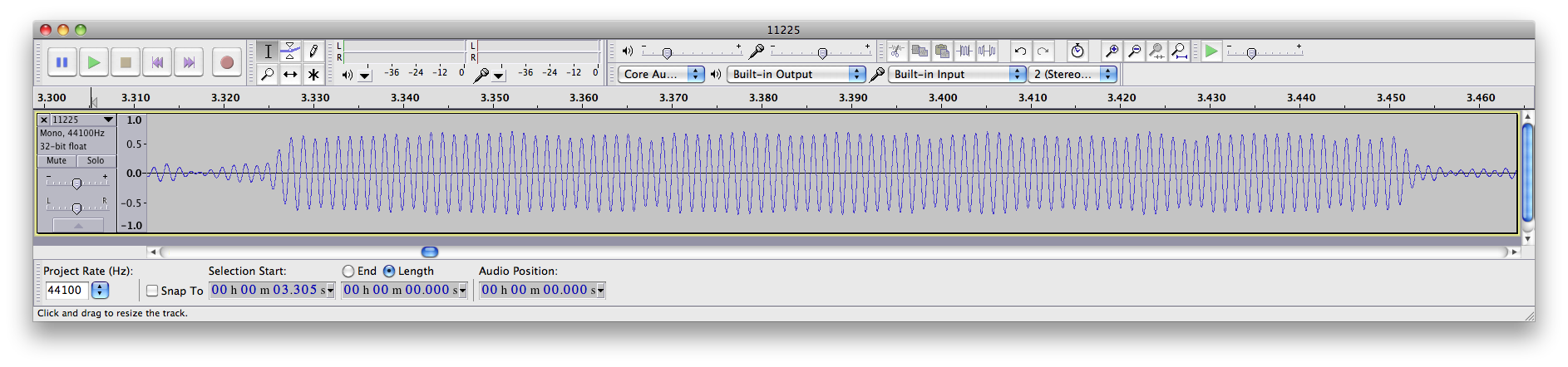
Next, here’s a recording from the Canadian time station, CHU:

The delay for the CHU pulse is 401 samples. Subtracting the radio delay of 286 gives us a delay due to propagation of 115 samples. Multiplying by our conversion factor of 22.676 microseconds per sample gives us 2607 microseconds. We’ll do our next multiplication again, to convert to distance:
2607 * 0.186 = 486 miles (782 km)
The actual distance from my location to CHU is 407 miles, or 656 km.
Now let’s try to take into account the actual path of the radio waves, which get reflected off the ionosphere. We need to know the height of the ionosphere, which unfortunately is not constant, nor is it the same over each part of the Earth. Here is a map showing the approximate height, while the above recordings were taken:
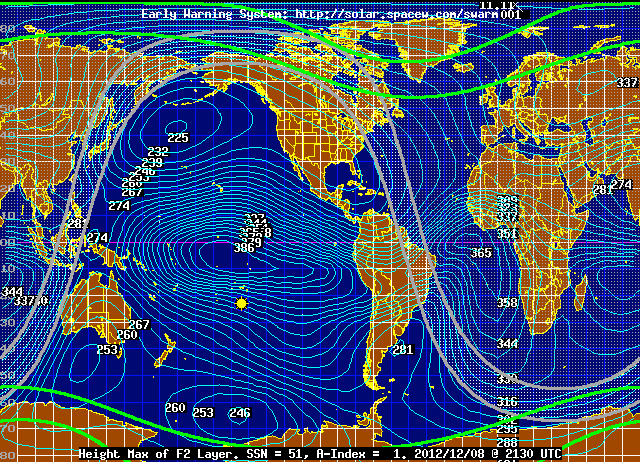
In the case of the path to CHU, the height is about 267 km, or 166 miles.
We also need to determine the straight line path between my location and CHU, through the Earth, vs the distance along the Earth’s surface. This can be calculated, and it is 391 miles, or 629 km.
We’ll determine what the actual path length is for a radio signal traveling this distance. It looks like a triangle, with a height of 166 miles, and a base of 391 miles. We need to determine the other two sides to find the total path length. All we need to do is take half of 391 miles, which is 195.5 miles, square it, add to that 166 squared, and take the square root, then double our answer. The result is 513 miles, which is very close to our measured value of 486 miles. We’re off by a little more than 5%.
Next let’s try WWV: The actual distance is 1468 miles or 2362 km. Doing our math, using an approximate FoF2 ionosphere height of 246 km (153 miles): Half of 1468 miles is 734 miles, we square that and add to 153 squared, and take the square root, and double our answer, getting 1500 miles. Our measured distance was 1567 miles, so we’re off by less than 5%.
Next, the case of WWVH. This is more complicated, as the signal probably is making more than one “hop”, that is, it is going up to the ionosphere, reflected down to Earth, and then reflected back up again, and down again. This may possibly occur multiple times.
We’ll try doing the math anyway. The actual distance is 4588 miles or 7383 km. Doing our math, using an approximate FoF2 ionosphere height of 253 km (157 miles): Half of 4588 miles is 2294 miles, we square that and add to 157 squared, and take the square root, and double our answer, getting 4598 miles. Our measured distance was 5339 miles, an error of 16%. But again, we don’t know how many hops there were. Still, not a bad effort.
Does anyone else have a GPS receiver with a 1 PPS output? If so, I’d like to hear from you, I have some additional experiments in mind.