In Measuring The Distance To A Shortwave Radio Station we looked at how the propagation delay in a shortwave signal can be used to estimate the distance to the station.
I ran some more tests the other day:
Below is a recording of 15 MHz, taken at 2300 UTC on December 13, 2012:
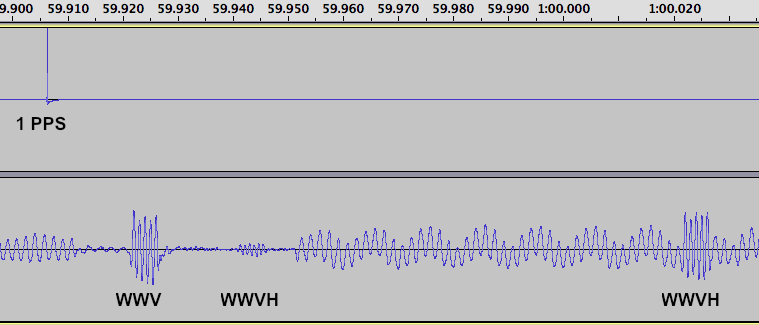
The GPS 1 PPS reference is on the top trace, and the audio from the radio is on the lower trace.
You can see the one second tick pulse from WWV in the audio, as well as two pulses from WWVH, the first (weaker) one is the normal (short) path signal, and the second one is via long path. We can confirm this is the case by converting the time delays into distance. We’ll use the same formula as in the previous article, we subtract off the 286 sample delay from the radio, multiply by 22.676 to convert the delay in samples to microseconds, then multiply by 0.186282 (the speed of light in miles per millisecond) to convert the delay into miles.
For WWV, the measured delay from the 1 PPS pulse is 660 samples. (660-286) * 22.676 * 0.186282 = 1580 miles
For WWVH short path, the measured delay was 1516 samples: (1516-286) * 22.676 * 0.186282 = 5196 miles
For WWVH long path, the measured delay was 5080 samples: (5080-286) * 22.676 * 0.186282 = 20250 miles
The distance to WWV is 1480 miles, and to WWVH is 4743. The long path distance to WWVH is 20158 miles.
Remember, the calculated distances can be longer than the great circle distance, due to the signal making one or more (many more in the case of long path) hops between the Earth and the ionosphere. Plus, there is the experimental error.
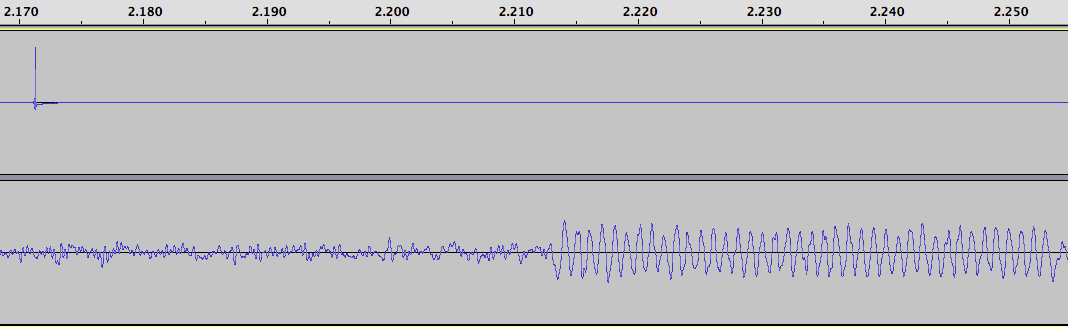
And here is one more example, this time it is the Russian time station RMW, on 14996 kHz, recorded at 1157 UTC on December 10, 2012:
The delay was 1835 samples: (1835-286) * 22.676 * 0.186282 = 6543 miles.
The great circle distance is 4821 miles.